De foutmarge berekenen, formule en voorbeelden
Ontdek hoe u foutmarges bepaalt en onze online calculator gebruikt om deze direct te meten.
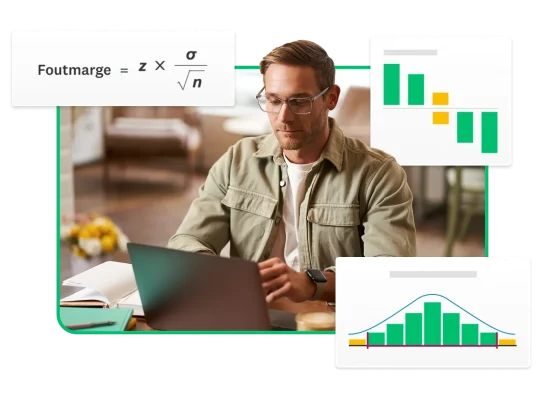
- De foutmarge geeft aan hoe betrouwbaar enquêteresultaten zijn. U ziet in hoeverre de steekproefresultaten kunnen verschillen van de gehele populatie.
- De foutmarge wordt berekend met de volgende variabelen: n = steekproefgrootte • σ = standaardafwijking van populatie • z = z-score (u kunt ook de onderstaande calculator gebruiken).
- Met de calculator voor de foutmarge kunt u bepalen of uw steekproefgrootte voldoende is om de door u verzamelde gegevens te vertrouwen.
Uw foutmarge berekenen
Populatieomvang
Betrouwbaarheidsniveau (%)
Steekproefgrootte
Foutmarge
0
Wat is een foutmarge?
Enquêtes zijn een evenwichtsoefening: U gebruikt een kleine groep (uw respondenten) om een veel grotere (de doelmarkt of de totale populatie) te vertegenwoordigen. De foutmarge is een statistische maatstaf van hoe nauwkeurig de resultaten van een enquête een afspiegeling zijn van de populatie als geheel.
De foutmarge meet hoe nauwkeurig uw enquête is. Hoe kleiner de foutmarge, hoe meer u op de resultaten kunt vertrouwen. Hoe groter de foutmarge, hoe minder zeker het is dat u de mening van de totale populatie vat.
De foutmarge is een bereik van waarden rondom de resultaten van de enquête. Als bijvoorbeeld 60% het antwoord 'ja' kiest met een foutmarge van 5% bij een betrouwbaarheidsniveau van 95%, is de kans 95% dat 55% tot 65% van de populatie 'ja' zou kiezen.
De foutmarge is onmisbaar in onderzoek en enquêtes, aangezien deze aangeeft hoe betrouwbaar de resultaten zijn. We weten beter wat de mate van onzekerheid is in onze bevindingen en kunnen de gegevens beter interpreteren. Een kleinere foutmarge duidt op een hogere mate van precisie en betrouwbaarheid van de resultaten, terwijl een hogere marge op meer variabiliteit en minder betrouwbaarheid wijst.
Uiteindelijk kunnen onderzoekers en besluitvormers met de foutmarge onderbouwde beslissingen nemen die zijn gebaseerd op de betrouwbaarheid van de gegevens.
Wat is een betrouwbaarheidsinterval?
Betrouwbaarheidsintervallen zijn een manier om het bereik te schatten waarin we denken dat de daadwerkelijke resultaten zich bevinden. Als we bijvoorbeeld de gemiddelde lengte schatten van alle individuen in een land, dan krijgen we met een betrouwbaarheidsinterval het bereik van de lengtes waarin vrijwel zeker het echte gemiddelde ligt.
Uit de betrouwbaarheidsintervallen kunnen onderzoekers en besluitvormers de onzekerheid afleiden die aan hun schattingen en analyses is gekoppeld.
De verhouding tussen foutmarges en betrouwbaarheidsintervallen
Een betrouwbaarheidsinterval en de foutmarge zijn eigenlijk twee verschillende manieren om hetzelfde concept uit te drukken: De onzekerheid die gepaard gaat met enquêteschattingen. Het betrouwbaarheidsinterval biedt een reeks met waarden waarvan we weten dat hierbinnen de echte waarde ligt. De foutmarge biedt een specifieke maatstaf van in hoeverre de schatting verwijderd is van de echte waarde.
Een verwant maar ander concept is het betrouwbaarheidsniveau. Uit het betrouwbaarheidsniveau kunnen we afleiden hoe zeker we weten dat de echte waarde zich binnen het interval bevindt.
Veelvoorkomende betrouwbaarheidsniveaus zijn 90%, 95% en 99%. Bij een lager betrouwbaarheidsniveau, zoals 90%, krijgen we een nauwer betrouwbaarheidsinterval. Hoe nauwer het interval, hoe nauwkeuriger onze schatting is. Maar bij een lager betrouwbaarheidsniveau is de kans kleiner dat we de echte waarde vastleggen. Als het betrouwbaarheidsniveau daarentegen hoger ligt, zoals 99%, krijgen we een breder betrouwbaarheidsinterval. Dit bredere interval is minder nauwkeurig, maar de kans is groter dat de juiste waarde wordt gevonden.
Wanneer gebruikt u een foutmarge?
U dient de foutmarge te gebruiken als u uw enquête plant om zo nauwkeurige en betrouwbare resultaten te garanderen. Door de foutmarge te kennen, kunt u de steekproefgrootte berekenen die u nodig hebt om de gewenste precisie te krijgen voor uw enquêteschattingen. Voor een kleinere foutmarge hebt u een grotere steekproef nodig, terwijl u voor een grotere foutmarge een kleinere steekproef kunt gebruiken.
Als een onderzoeker bijvoorbeeld een enquête wil uitvoeren onder een populatie van 100.000 mensen met een foutmarge van ±5% en een betrouwbaarheidsniveau van 95%, dan is een steekproefgrootte van ongeveer 383 respondenten vereist (berekend met de standaardformules).
Ook is de foutmarge essentieel bij de interpretatie van enquêtebevindingen. De marge is een maatstaf van de onzekerheid van de resultaten. Onderzoekers en belanghebbenden kunnen de betrouwbaarheid van de conclusies beoordelen.
Als bijvoorbeeld uit een enquête blijkt dat 60% van de respondenten een voorkeur heeft voor product A in plaats van product B, en de foutmarge is ±3% bij een betrouwbaarheidsniveau van 95%, dan is de kans groot (95%) dat het echte deel van de mensen met een voorkeur voor product A tussen de 57% en 63% ligt.
Wat is de formule voor het berekenen van de foutmarge?
Dit is de formule om de foutmarge te berekenen:
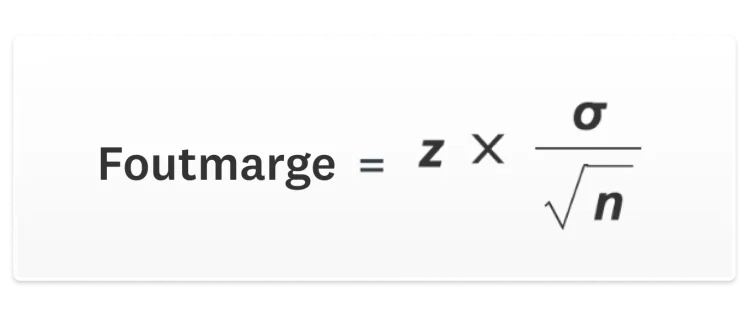
n = steekproefgrootte • σ = standaardafwijking van de populatie • z = z-score
- Neem de standaardafwijking van de populatie (σ) en de steekproefgrootte (n). De bovenstaande calculator gaat uit van een standaardafwijking die is gebaseerd op de vierkantswortel van p(1-p), waarbij p de proportionele steekproef en p = 0,5 een behoudende standaard is.
- Bereken de vierkantswortel van de steekproefgrootte en deel deze door de standaardafwijking van de populatie.
- Vermenigvuldig de uitkomst met de z-score van het gewenste betrouwbaarheidsniveau overeenkomstig de volgende tabel.
| Gewenst betrouwbaarheidsniveau | z-score |
| 80% | 1,28 |
| 85% | 1,44 |
| 90% | 1,65 |
| 95% | 1,96 |
| 99% | 2,58 |
Voorbeeld van een foutmargeberekening
Stel u wilt kiezen tussen naam A en naam B voor een nieuw product en uw doelmarkt bestaat uit 400.000 potentiële klanten. Dit is uw totale populatie.
U besluit 600 van deze potentiële klanten te enquêteren. Dat is uw steekproefgrootte.
Wanneer de resultaten binnen zijn, blijkt dat 60% van de respondenten een voorkeur heeft voor naam A. U moet een betrouwbaarheidsniveau invoeren in de foutmargecalculator.
Dit getal geeft aan hoe zeker u weet dat de steekproef nauwkeurig de mening van de totale populatie vertegenwoordigt. Onderzoekers stellen dit doorgaans in op 90%, 95% of 99%.
Voer de cijfers van het voorbeeld hierboven in de foutmargecalculator in. De calculator geeft u een foutmarge van 4%.
Dus 60% van uw respondenten koos voor naam A. De foutmarge betekent dat u nu met een zekerheid van 95% weet dat 56% tot 64% van de totale populatie (uw doelmarkt) de voorkeur geeft aan naam A voor uw product.
Wij komen op 56 en 64 uit door de foutmarge op te tellen bij en af te trekken van uw steekproef.
De foutmarge interpreteren
De foutmarge geeft een bereik van waarden rondom de schatting van een enquête en toont zo de mate van onzekerheid. Stel een enquête beweert dat 60% een beleid ondersteunt en de foutmarge ligt op ±4% bij een betrouwbaarheidsniveau van 95%. Dan kunnen we redelijkerwijs de conclusie trekken dat het echte percentage tussen de 56% en 64% ligt.
Factoren met invloed op de foutmarge
1. Steekproefgrootte
De steekproefgrootte heeft in enquêtes een rechtstreekse impact op de foutmarge. Grotere steekproeven leiden gewoonlijk tot kleinere foutmarges. En kleinere steekproeven hebben meestal grotere foutmarges.
Zo kan een enquête met 1000 respondenten een foutmarge hebben van ±3%. Is de steekproef twee keer zo groot, dan kan de foutmarge dalen naar ±2%.
Verder lezen: Steekproefcalculator
2. Betrouwbaarheidsinterval
Een hoger betrouwbaarheidsniveau leidt tot een grotere foutmarge. Lagere betrouwbaarheidsniveaus gaan gepaard met kleinere foutmarges.
Een enquête met een betrouwbaarheidsniveau van bijvoorbeeld 95% kan een foutmarge hebben van ±3%. Stijgt dat betrouwbaarheidsniveau naar 99%, dan kan de foutmarge ±4% worden.
3. Variabiliteit in de populatie
Bij een grotere variabiliteit in de populatie krijgt u grotere foutmarges. Bij minder variabiliteit worden de marges kleiner.
Schattingen over het inkomen in een stad met flinke inkomensverschillen kunnen bijvoorbeeld een grotere foutmarge vereisen, zoals ±€ 5000. En een stad met minder spreiding van de inkomens kan een kleinere marge hebben, zoals ±€ 2000.
De betrouwbaarheid van uw gegevens verhogen

Nu u weet hoe de foutmarge wordt berekend en welke invloed die heeft op uw resultaten, kunnen wij u de stappen laten zien om deze concepten in uw enquête-ontwerp op te nemen.
1. Bepaal uw totale populatie
Dit zijn alle mensen die u met uw enquête wilt onderzoeken, oftewel de 400.000 potentiële klanten van het vorige voorbeeld.
2. Kies het risiconiveau
U moet beslissen hoe groot het risico mag zijn dat uw resultaten afwijken van de mening van de gehele doelmarkt. Dit betekent dat u de foutmarge en het betrouwbaarheidsniveau voor uw steekproef moet meten.
3. Geef de steekproef op
Nadat u een evenwicht hebt gevonden tussen het betrouwbaarheidsniveau en de foutmarge die u acceptabel vindt, moet u kiezen hoeveel respondenten u wilt ondervragen. En onthoud dat niet iedereen die een uitnodiging voor de enquête krijgt, de enquête ook invult: uw steekproefgrootte is het aantal volledig ingevulde enquêtes dat u terugontvangt.
4. Bereken het reactiepercentage
Het reactiepercentage bestaat uit de feitelijke respondenten van degenen die uw enquête hebben ontvangen. U kunt uw eerdere enquêtes erbij pakken om uw gebruikelijke reactiepercentage te zien. Hebt u geen eerdere enquêtegegevens, dan kunt u een schatting doen. Een behoudend percentage is dat ongeveer 10% tot 15% zal deelnemen aan de enquête.
5. Doelgroep van de enquête
Zodra u het percentage van stap 4 hebt, weet u naar hoeveel mensen u de enquête moet sturen om het gewenste aantal voltooide reacties uit stap 3 te ontvangen. Wij hebben gezien dat de foutmarge (en alle verwante concepten, zoals steekproefgrootte en betrouwbaarheidsniveau) belangrijk zijn om bij het ontwerp van de enquête een goede balans te vinden. Als u die kunt berekenen, kunt u vol overtuiging aan de slag.
Verder lezen: Uw populatie schatten
Uw foutmarge verbeteren met SurveyMonkey
Met SurveyMonkey kunt u uw steekproefgrootte uitbreiden en uw foutmarge verkleinen. SurveyMonkey Audience heeft een krachtig platform waarmee u snel en efficiënt gegevens van een hoge kwaliteit kunt verzamelen bij een doelgroep die aansluit op uw doelmarkt. Of u nu een nieuw product op de markt brengt, de klanttevredenheid meet of academisch onderzoek uitvoert, ons platform heeft de tools waarmee u uw doelgroep bereikt en reacties verzamelt waar u echt wat aan hebt.
De juiste gegevens verzamelen
SurveyMonkey biedt u de tools die u nodig hebt voor het maken, optimaliseren en delen van uw enquêtes zodat u de reacties krijgt die u nodig hebt.