T-toetsen uitgelegd: wat betekenen ze voor enquêteanalyse?

Iedereen kan wel het verschil zien tussen twee getallen. Maar het is lastiger om te achterhalen of dit verschil echt statistisch significant is.

Stel dat u een klanttevredenheidsenquête houdt voor uw bedrijf en u hebt een schat aan resultaten die u wilt analyseren. U vraagt uw baas wat het belangrijkst is en zij wil graag weten of vrouwen en mannen een ander antwoord geven. Geven mannen bijvoorbeeld gemiddeld een lagere Net Promoter Score℠ (NPS) dan vrouwen?

Als u de gegevens bekijkt, ziet u dat de gemiddelde score van mannelijke respondenten een 9 was en die van vrouwen een 12. Hoe weet u of 9 een significant verschil is met 12? Daar komt de t-toets bij om de hoek kijken.

Met de t-toets kunt u bepalen of twee getallen significant van elkaar verschillen. Er zijn verschillende t-toetsen, die elk worden berekend met een andere formule.

1. T-toets voor één steekproef: met deze toets ziet u of het gemiddelde van de gegevens in één groep (in dit geval de totale NPS) afwijkt van een door u opgegeven waarde.

Voorbeeld: uw bedrijf wil een NPS behalen die significant hoger is dan de sectornorm van 5. In de meest recente enquête van uw bedrijf is de NPS 10. Is dit significant hoger dan de sectornorm van 5?

2. T-toets voor twee steekproeven: met deze toets onderzoekt u of de gemiddelden van twee onafhankelijke groepen significant van elkaar verschillen. Deze toets wordt ook de ongepaarde t-toets of onafhankelijke t-toets genoemd.

Uw hypothese is bijvoorbeeld dat mannen uw bedrijf een lagere NPS geven dan vrouwen. De gemiddelde NPS van mannelijke respondenten is 9, terwijl vrouwen een gemiddelde score van 12 geven. Is 9 significant lager dan 12?

3. Gecombineerde t-toets: deze toets gebruikt u als u dezelfde enquête twee keer afneemt bij dezelfde groep. Met een gecombineerde t-toets kunt u zien of het gemiddelde tussen de eerste en tweede enquête is veranderd. Deze toets wordt ook de gepaarde t-toets genoemd.

U hebt een enquête bijvoorbeeld twee keer afgenomen bij dezelfde groep klanten: de eerste keer in april en de tweede keer in mei, nadat ze een advertentie voor uw bedrijf hadden gezien. Is de NPS van uw bedrijf veranderd nadat uw klanten de advertentie hebben gezien?

Met een t-toets kunt u vaststellen of iets significant verschilt. Maar u moet zelf bepalen of dat verschil iets betekent. Een klein verschil kan statistisch gezien significant zijn als de steekproef groot genoeg is.

Een t-toets bestaat uit vier stappen:

1. De t-statistiek berekenen:
Elke soort t-toets heeft een andere formule voor het berekenen van de t-statistiek (blader naar de onderkant van de pagina om de drie formules te zien).

2. De vrijheidsgraden berekenen: 
De vrijheidsgraden zijn het aantal manieren waarop het gemiddelde kan variëren. In dit geval zijn de vrijheidsgraden het aantal NPS-beoordelingen dat u kunt ontvangen van een bepaalde groep respondenten. Net als met de t-toets is de formule voor vrijheidsgraden afhankelijk van het type t-toets dat u gebruikt.

3. De kritieke waarde bepalen: 
De kritieke waarde is de grenswaarde waarbij het verschil tussen twee getallen als statistisch significant wordt gezien.

4. De absolute waarde van de t-statistiek vergelijken met de kritieke waarde: 
Als de t-statistiek groter is dan uw kritieke waarde, is het verschil significant. Als de t-statistiek kleiner is, dan zijn uw cijfers statistisch gezien gelijk.

We pakken het voorbeeld van het begin er weer bij: uw hypothese is dat mannen uw bedrijf een lagere NPS geven dan vrouwen. De gemiddelde NPS van mannelijke respondenten is 9, terwijl vrouwen een gemiddelde score van 12 geven. Is 9 significant lager dan 12? Hiervoor kunt u de t-toets voor twee steekproeven gebruiken.

1. T-statistiek berekenen: 

Hieronder staat de formule voor de t-toets met twee steekproeven waarbij:

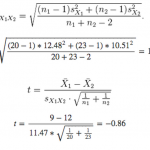
2. De vrijheidsgraden berekenen: 

Deze formule moet worden gebruikt om de vrijheidsgraden in t-toetsen met twee steekproeven te berekenen. De formules voor de andere toetsen staan hieronder.

3. De kritieke waarde bepalen: 

Volgens deze tabel geldt voor een tweezijdige toets met een alfawaarde van 0,05 en 41 vrijheidsgraden een kritieke waarde van 2,02. De meeste analisten gebruiken een tweezijdige toets in plaats van een eenzijdige toets, omdat deze conservatiever is. Wilt u meer uitleg over de t-toets? Bekijk voor meer informatie over de verschillen tussen eenzijdige en tweezijdige toetsen deze video van de Khan Academy.

4. De absolute waarde van de t-statistiek vergelijken met de kritieke waarde: 

Aangezien de absolute waarde van de t-statistiek 0,86 is (niet groter dan de kritieke waarde van 2,02), kunt u concluderen dat mannen niet significant lagere NPS-scores geven dan vrouwen.

U voert de t-toetsen waarschijnlijk uit in een spreadsheet of statistisch programma (zoals Excel of SPSS). Als u de berekeningen handmatig wilt doen, vindt u hieronder de formules voor de andere twee soorten t-toetsen. Bij sommige betaalde abonnementen is het ook mogelijk om de enquêteresultaten te exporteren voor gebruik in SPSS (Statistical Package for the Social Sciences), een populair computerprogramma dat wordt gebruikt voor statistische analyse. Om de t-toets SPSS functie te gebruiken, dienen de gegevens wel aan bepaalde criteria te voldoen.

Wilt u (zoals de meeste mensen) de t-toetsen in een spreadsheet of statistisch programma uitvoeren, dan is het proces iets anders. In plaats van de t-statistiek te vergelijken met de kritieke waarde, berekenen de meeste programma's een p-waarde. Deze waarde wordt vergeleken met uw alfawaarde (de meestgebruikte waarde is 0,05). In dit geval geeft een p-waarde die onder uw alfawaarde ligt aan dat de getallen significant verschillend zijn.

Net Promoter Score is een handelsmerk van Bain & Company, Inc., Satmetrix Systems, Inc. en F. Reichheld.